VAE paper

2025年9月12日

9:03

 

X表示图片数据集，表示一张图片。假设的生成过程中涉及到某个未被观测到的连续随机变量z，的生成过程分为 两步：

1）从某个分布中采样生成

2）再从条件分布中生成

 

 

我们用来近似真实后验，也被称为probabilistic encoder，因为给定一个x，输出的是关于z的概率分布。也被称为probabilistic decoder，因为给定一个z，输出的是关于x的概率分布。

 

也就是说，我们既想要求得作为我们的encoder，又想要求得作为我们的decoder。求分布的参数，还是通过极大似然法。

似然函数：

 

从式（2）看出，似然函数可以写成2部分，第一项是KL散度，第二项叫做ELBO，

 

1 ELBO:

其中，ELBO可以写成上图中公式（2）和公式（3）两种形式，

• 对于公式（2）来说，是一个期望，期望可以通过monte carlo 采样得到估计值，但是这个估计的方差太大，无法使用（具体推导不清楚）。最关键的是，采样的过程是不可导的，我们想求得L对分布参数的导数，但是L中包含期望，求期望需要我们进行采样来估计这个期望，而采样涉及到从这个分布中采样得到z，这个过程是对是不可导的。

 

 

我们可以用重参数化技巧：公式（4），将原来的变成，也就说，原来的z是从这个分布中采样得到的，重参数化之后，z是由函数得到的。经过公式（4）重写之后，公式（2）的估计值可以写成公式（6）的形式，这个估计值的方差就变小了？，关键是使L对参数变得可导了。

• 对于式（3）来说，同样有一个期望项，这个期望也通过重参数化技巧变得可导了。公式（3）由2项组成，第一部分是KL散度，也可以看作是正则项，约束probabilistic encoder逼近先验。第二部分可以看作是auto encoder中的重构误差。且在实验中，采样的步数L可以只设置为1步，只要batch_size足够大即可。

 

 

2 关于重参数化：

 

 

重参数化使得采样过程变得可导，以高斯分布为例，原来的，重参数化之后，z=u+，这就使得整个损失函数变得可导了。

关于如何选择重参数化的函数g，（这部分懒得看）

 

 

3 Example: Variational Auto-Encoder

假设隐变量z的先验是标准高斯分布，N(z; 0; I)，并假设probalistic encoder   和 probalistic decoder 都是高斯分布，这两个分布的参数（均值、方差）分别由神经网络拟合得到。

 

 

式（10）即式（7）,ELBO的第二种形式，式（10）的LOSS分为两部分，第一部分是probalistic encoder的loss，由于是高斯分布，所以可以写成这样的形式，神经网络的输入是x(i)，输出的是probalistic encoder   这个高斯分布的均值和方差。第二部分是probalistic decoder的loss，由于假设了 probalistic decoder 是高斯分布，所以这一项  是可以写成解析形式的公式，神经网络的输入是z(i)，输出是probalistic decoder 这个高斯分布的参数，即均值和方差，然后将均值方差代入高斯分布的概率密度公式，得到

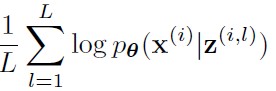
这一项的结果。那么z(i)是如何得到的呢，z(i)理论上是通过从   这个分布中采样得到的，但是这样的话，整个loss不可导，所以通过重参数技巧得到z,z=u+，其中u和是probalistic encoder 的均值和方差。